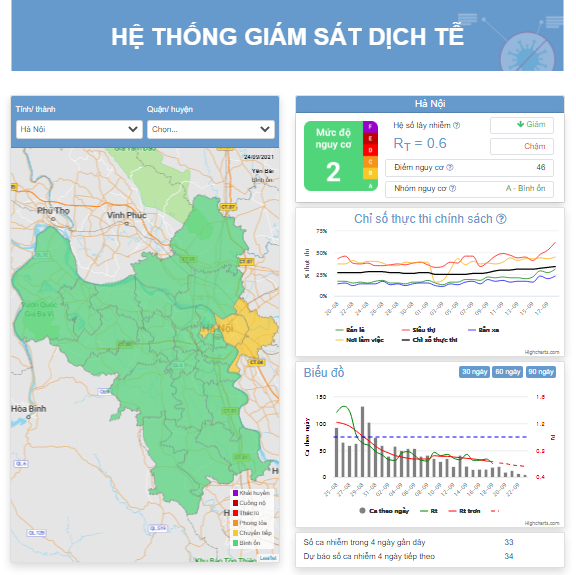
Trong bài này chúng tôi bàn thêm về khoảng thời gian nối tiếp (serial interval) và số ca được báo cáo (reported case). Đây là các khái niệm quan trọng nhưng đôi khi bị hiểu nhầm.
Chi tiết về mô hình xem thêm phần Thông tin hoặc trực tiếp tại đây
1. Khoảng thời gian nối tiếp
Ở Việt Nam, khoảng thời gian nối tiếp (KTGNT) hay được hiểu nôm na là chu kỳ lây nhiễm. Chúng tôi đã đề cập về khoảng thời gian nối tiếp trong loạt bài viết trước. Trong bài viết này, chúng tôi trích dẫn các nghiên cứu khoa học và bàn luận về các ước lượng cho KTGNT của chủng Delta.
Chúng tôi đã trình bày hơn một năm trước về KTGNT trong báo cáo tháng 06/2020. Thông tin mà ta thực sự cần là thời điểm bị nhiễm bệnh và khoảng thời gian sinh (generation interval). Do ta không thể quan sát các biến số đó, ta thay thế thời điểm bị nhiễm bệnh bởi thời điểm khởi phát bệnh, và khoảng thời gian sinh bởi KTGNT.
Chúng tôi không ước lược trung bình (hay trung vị) của KTGNT, được kí hiệu là T trong bài này, mà tham khảo các nghiên cứu khoa học. Nguyên nhân chính là chúng tôi không có dữ liệu cần thiết để làm. Tuy nhiên chúng tôi có các phương pháp để xác định T được ước lượng có đủ chính xác hay không. Sử dụng T được ước lượng sai sẽ dẫn đến một dự báo có sai số lớn (cả phương pháp ước lượng thô và phương pháp SEIR), một ước lượng đỉnh dịch địa phương bị lệch, và tốc độ thay đổi của hệ số lây nhiễm quá nhanh hay quá chậm.
1.1 Một phương pháp đơn giản để tìm cận dưới của T
Ta xét một phương pháp đơn giản để thấy vì sao T quá nhỏ là vô lý. Hệ số lây nhiễm cơ bản R0 của chủng Delta cho nhiều xã hội được xác định là khoảng 5. Như đã đề cập trong bài viết 1, trong giai đoạn đầu n*T ngày, nếu R0 > 1, trung bình 1 cá thể bệnh sinh ra tổng số cá thể bệnh:
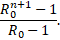
n hay được gọi nôm na là số chu kỳ lây nhiễm. Chúng ta thường phát hiện ra một ổ dịch khi nó đã có ít nhất 10 ngày. Với 10 ngày, ta có n = 10/T. Bảng dưới cho tổng số ca sau 10 ngày với R0 = 5 và các giá trị khác nhau của T.
|
T (ngày) |
n |
Số chu kỳ lây nhiễm |
Tổng số ca sau 10 ngày |
|
4 |
2,5 |
2 - 3 |
31 - 156 |
|
3 |
3,3 |
3 - 4 |
156 - 781 |
|
2 |
5 |
5 |
3906 |
|
1 |
10 |
10 |
> 12 triệu |
|
1/2 ngày (12h) |
20 |
20 |
> 119 nghìn tỉ |
|
1/3 ngày (8h) |
30 |
30 |
> 1 nghìn tỉ tỉ |
|
1/6 ngày (4h) |
60 |
60 |
> 1 triệu tỉ tỉ tỉ tỉ |
|
T (ngày) |
n |
Số chu kỳ lây sau 7 ngày |
Tổng số ca sau 7 ngày |
|
1/2 ngày (12h) |
14 |
14 |
7,6 tỉ ~ 98% dân số thế giới |
Từ bảng trên ta thấy T ≤ 2 là phi thực tế đối với xã hội bị nhiễm chủng Delta với R0 = 5. Nếu T = 1 thì toàn Hà Nội hoặc TP. Hồ Chí Minh đạt miễn dịch cộng đồng trong ít hơn 10 ngày nhưng thực tế không cho thấy điều đó.
Nếu T là 12 tiếng thì hơn 98% dân số cả quả đất đã nhiễm trong 7 ngày, dịch qua đi trong 1 tuần. Chúng ta có thể dễ dàng liên tưởng điều này với T=12h là chu kỳ lây nhiễm của T-virus gây ra đại dịch Zombie trong tưởng tượng của các nhà làm phim Hollywood.
Trong khi nếu T là 8 tiếng thì toàn bộ dân số cấp độ vũ trụ khả kiến đạt miễn dịch cộng đồng sau 10 ngày, và nếu T là 4 tiếng thì toàn bộ dân số cấp độ vũ trụ toàn thể cộng với một số rất lớn các vũ trụ khác trong đa vũ trụ đạt miễn dịch cộng đồng sau 10 ngày. Chuyên gia nào tư vấn T từ 4-8 tiếng chắc có tầm nhìn xa đa vũ trụ.
1.2. Lược sử nghiên cứu (literature review)
Tiếp theo chúng tôi trích dẫn và bình luận các báo cáo khoa học để cho thấy vì sao T = 4 ngày là đúng. Bạn xem phần phụ lục có 5 báo cáo khoa học được xem xét.
Trước tiên chúng ta thấy rằng báo cáo khoa học đầu tiên về T là từ Public Health England vào 27/05/21, và họ ước lượng ra 4 hoặc 5 ngày. Hai tuần sau với dữ liệu lớn hơn, họ cập nhật là 4 ngày.
Tiếp theo chúng ta thấy rằng mọi báo cáo đều cho T ≥ 2,3 ngày, nên nếu chuyên gia nào tư vấn T chỉ 8 tiếng thì nó không dựa trên một nghiên cứu khoa học công khai nào mà chúng tôi được biết.
Bây giờ chúng ta bàn về chuyện vì sao nhiều người cho rằng giá trị của T chỉ nhỉnh hơn 2. Ngày 27/05, báo cáo của Public Health England ước lượng ra T từ 4-5 (với số mẫu là 618 cặp lây nhiễm trong hộ gia đình và 160 cặp ngoài hộ gia đình). Tuy nhiên tài liệu của Public Health England không dễ tìm kiếm bằng Google hay Google Scholar nên ít người biết. Ngoài tài liệu của Public Health England, trước 13/08, chỉ còn 2 báo cáo khác của Singapore và Trung Quốc. Hai báo cáo này lại rất dễ tìm ra với Google Scholar. Ngày 04/06, báo cáo của Singapore ước lượng ra T = 3 (với số mẫu là 32 cặp trong hộ gia đình). Ngày 24/06, báo cáo của Trung Quốc ước lượng ra T = 2,3 (với số mẫu là 68 cặp). Việc dễ tìm ra hai báo cáo này mà khó tìm ra báo cáo từ Public Health England là nguyên nhân chính nhiều người cho rằng T chỉ khoảng 2 đến 3. Đã thế, ngày 20/8, lại có một báo cáo từ Hàn Quốc ước lượng ra T = 2,5 với số mẫu lớn (1599 cặp).
Tuy nhiên 2 trong 3 báo cáo trên đã được sửa chữa sau đó. Ngày 13/8, báo cáo của Trung Quốc được sửa chữa với T từ 5,8 rồi giảm xuống 4 trong 10 ngày (7 tác giả trong bài báo ngày 24/06 cũng là tác giả trong bài báo ngày 13/8, bao gồm cả 2 first authors trong cả 2 bài). Ngày 6/10, báo cáo của Hàn Quốc sửa từ 2,5 lên 3,5 sau khi hiệu chỉnh dữ liệu. Báo cáo của Singapore vẫn giữ nguyên, nhưng đã kết luận không có bằng chứng rằng T thay đổi so với chủng cũ.
2. Dự báo số ca được báo cáo
Nhiều người băn khoăn:
- Dự báo số ca để làm gì khi mà dữ liệu đâu có chính xác? Ví dụ như có khoảng 150.000 ca không được tính ở TP. Hồ Chí Minh (HCM) tháng 8-9/21, thì các dự báo chả có ý nghĩa gì.
- Làm sao để tính được số ca thực tế bị nhiễm bệnh ngoài cộng đồng?
Chúng tôi sẽ làm rõ các câu hỏi đó trong phần này. Về số ca theo ngày, ta có hai đại lượng:
- Số ca thực tế,
- Số ca được báo cáo (reported cases).
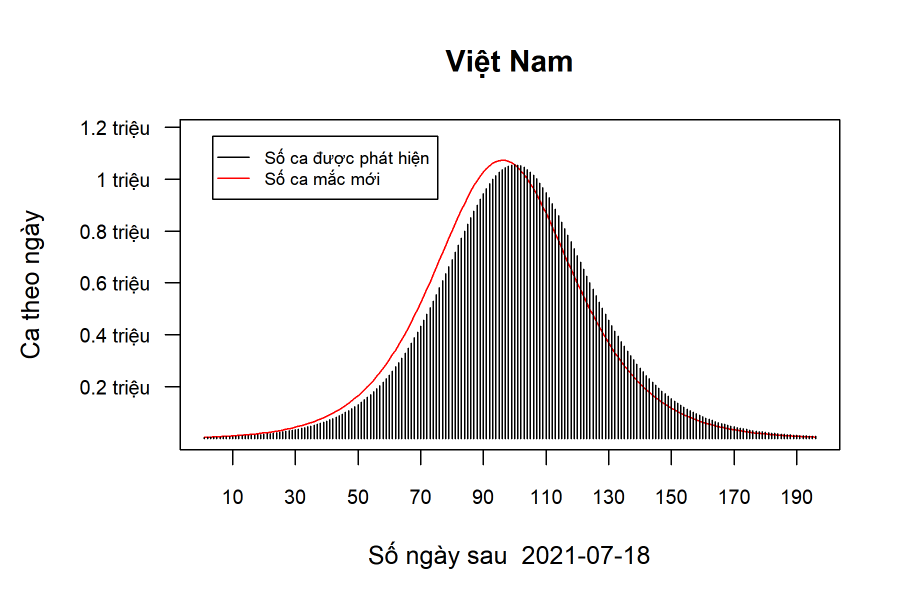
Nói ngắn gọn thì mỗi đại lượng có vai trò riêng của nó. Trước tiên để rõ ràng, chúng ta hiểu “số ca được báo cáo” là số ca được báo cáo từ Bộ Y tế (đôi khi cũng được gọi là “số ca được công bố”, hay "số ca được phát hiện", hay “số ca được quan sát”). Nó phụ thuộc vào năng lực phát hiện của hệ thống (truy vết, xét nghiệm, người ốm đến viện, v.v.). Còn “số ca thực tế” là số ca nhiễm thực sự.
2.1. Số ca được báo cáo
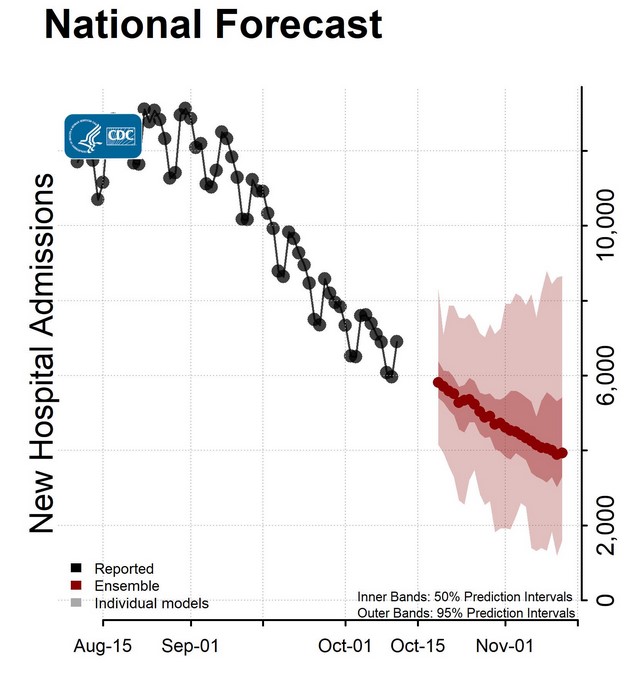
Trước tiên lấy một ví dụ. CDC Mỹ đã từng sử dụng hơn 100 mô hình dự báo cho COVID-19, và các mô hình đó dự báo số ca được báo cáo chứ không phải số ca thực tế. Họ đã mất công như vậy thì việc dự báo số ca được báo cáo phải có ý nghĩa nào đó. Bạn có thể cho rằng do số liệu ở Mỹ tốt nên nó mới có ý nghĩa. Không phải như vậy. Có những mô hình cho rằng số ca thực tế luôn gấp 2-5 lần số ca được báo cáo ở Mỹ.
Chúng tôi sẽ giải thích vì sao số ca được báo cáo là đủ cho việc kiểm soát dịch trong các giai đoạn nhất định. Mô hình chúng tôi có nhiều phần, thì phần nào cũng giả thiết rằng số ca thực tế có thể lớn gấp nhiều lần số ca được báo cáo.
- Kiểm soát dịch: Để kiểm soát dịch, biết xu hướng dịch lên hay xuống quan trọng hơn biết số ca là bao nhiêu. Như Hans Rosling nói “We were losing ourselves in details ... All we needed to know is, are the number of cases rising, falling, or leveling off?”. Xu hướng dịch lên hay xuống lại tương đương với R > 1 hay R < 1. Việc ước lượng R lại không cần số ca thực tế.
Xét một trường hợp để thấy điều này. Giả thiết số ca được báo cáo luôn tỷ lệ với số ca thực tế theo một tỷ lệ ξ nào đó. Ví dụ 30% số ca có triệu chứng thì số ca được phát hiện chiếm 30%. Giả sử hôm nay có 100 ca và chỉ 30% số đó, tức là 30 ca, được phát hiện. Giả sử hôm sau có 200 ca và cũng chỉ 30%, tức là 60 ca, được phát hiện. Khi đó 200/100 bằng 60/30. Tương tự vậy, do hệ số lây nhiễm R là một tỷ số, nó vẫn được tính đúng khi chỉ có số ca được báo cáo.
Trong thực tế ξ không cố định mà dao động ổn định quanh một đường ξ khi chiến lược xét nghiệm ít thay đổi trong thời gian quan sát, ví dụ, nếu chiến lược xét nghiệm là “Săn đuổi” tức là xét nghiệm truy vết chuỗi lây nhiễm F0-F1-F2 khi phát hiện ra F0, thì số lượng xét nghiệm thay đổi theo số cá thể liên quan có thể xác định được (F1-F2...), số lượng này biến thiên theo mức độ lây nhiễm của chuỗi lây nhiễm và tính phân phối mẫu theo thời gian bị cộng dồn theo đợt xét nghiệm; nhưng sự biến thiên này vẫn dao động quanh ξ còn biên độ của biến thiên là đặc tính của chiến lược xét nghiệm; trong khi nếu xét nghiệm định kỳ 100% dân số sẽ có số liệu ổn định và đều đặn nhất.
Chúng tôi đã phát triển một phương pháp để xác định RT-trơn trong điều kiện thực tế ξ không cố định mà dao động ổn định quanh một đường ξ với điều kiện chiến lược xét nghiệm ổn định trong thời gian quan sát.
Bây giờ bàn về 150.000 ca ở TP. HCM tháng 8-9/21. Số ca này được tạo ra bởi việc tăng xét nghiệm nhanh trong thời gian ngắn. Khi đó R bị mất ổn định một thời gian, sau đó lại ổn định trở lại (như trong báo cáo tại Viện Toán học ngày 26/08). Do chúng tôi ước lượng và hiểu quỹ đạo R, nên chúng tôi đã dự báo vào ngày 03/09 là tình hình HCM không đáng ngại dù số ca tăng lên cao nhất.
- Dập dịch: Giả sử số ca thực tế gấp 5 lần số ca được báo cáo. Khi mà số ca được báo cáo xuống 1, thì số ca thực tế cùng lắm là 5. Khi R < 1 nhiều ngày và số ca được báo cáo xuống 0 nhiều ngày, thì số ca ngoài kia cũng xuống 0. Như vậy ta dập được dịch. Điều này càng được củng cố bởi các nghiên cứu đã chỉ ra rằng chỉ khoảng 20-30% số ca là lây cho người khác, và một số ít hơn thế lây cho nhiều người (đúng với cả chủng Delta).
- Chuẩn bị ICU: Giả sử rằng mọi ca nặng cần ICU đều được quan sát. Gọi số ca thực tế là M ca, và ta chỉ quan sát được N < M ca. Khi đó Y/M = (Y/N) * (N/M) < Y/N. Nếu ta chuẩn bị số ICU theo tỷ lệ Y/N, thì ta luôn chuẩn bị theo tỷ lệ cao hơn tỷ lệ thật.
- Chuẩn bị hậu cần: Ta không thể sử dụng giường bệnh nếu ta không thể phát hiện ra bệnh nhân. Xét một ví dụ minh họa như sau. Giả sử ta không làm xét nghiệm gì cả, và 30% có triệu chứng luôn tới viện. Khi đó mô hình dự báo theo số ca đến viện, tức là 30% số ca thực tế. Nếu vẫn cứ 30% đến viện, thì mô hình dự báo đúng số giường cần chuẩn bị. Nếu ta chuẩn bị số giường theo số ca thực tế, thì ta chuẩn bị thừa 70% số giường do 70% không bao giờ đến viện.
- Realtime: Mô hình chạy realtime, nên cập nhật dự báo khi các tác động bên ngoài thay đổi. Khi ta tăng xét nghiệm, thì ta tìm thêm ra bệnh nhân. Nếu ta tăng xét nghiệm và duy trì mức xét nghiệm đó, thì mô hình sẽ cập nhật và tăng dự báo số ca được phát hiện.
2.2. Số ca thực tế
Bây giờ ta bàn về số ca thực tế. Trước đây khi tư duy theo 0 Covid, chúng ta luôn muốn chắc chắn rằng ngoài kia không còn F0 nào cả. Như đã nói ở trên, chỉ cần duy trì R > 1 trong thời gian đủ dài, và với số ca được báo cáo bằng 0 trong nhiều ngày, thì số ca thực tế ngoài cộng đồng cũng bằng 0. Do đó việc muốn biết số ca thực tế để dập dịch theo 0 Covid là không cần thiết. Hiện nay thì ta đã rõ là 0 Covid gần như không thể đạt được nữa trong vài năm tới.
Vậy biết số ca thực tế để làm gì? Các nước muốn biết số ca thực tế khi họ cần giải quyết các vấn đề như tính tỷ lệ tử vong do nhiễm bệnh (infection fatality ratio, hay IFR), hay tính miễn dịch cộng đồng. Các nước sử dụng serosurvey cho mục đích này vì không một mô hình nào khác có thể chính xác hơn.
3. Mô hình dự báo của một số quốc gia
Các nước có nền khoa học tiên tiến đều sử dụng các mô hình dự báo cho dịch COVID-19. Nhiều chính phủ không công khai các dự báo, nhưng các báo cáo khoa học về mô hình được công khai. Chúng tôi tham khảo một số nước dưới đây. Do thời gian có hạn nên chúng tôi chưa tham khảo được nhiều nước hơn nữa. Tuy nhiên trong quá trình tìm hiểu, chúng tôi có đọc báo cáo hoặc tin tức về mô hình của một số nước như Chile, Israel, Singapore, và Tây Ban Nha.
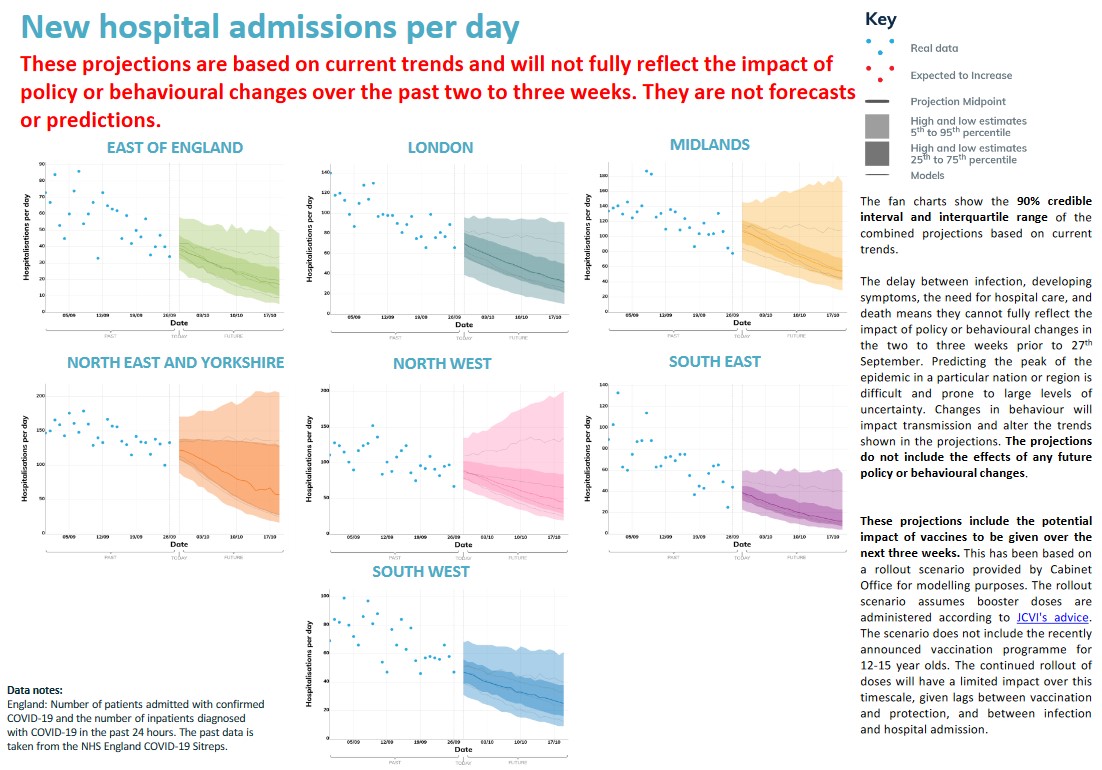
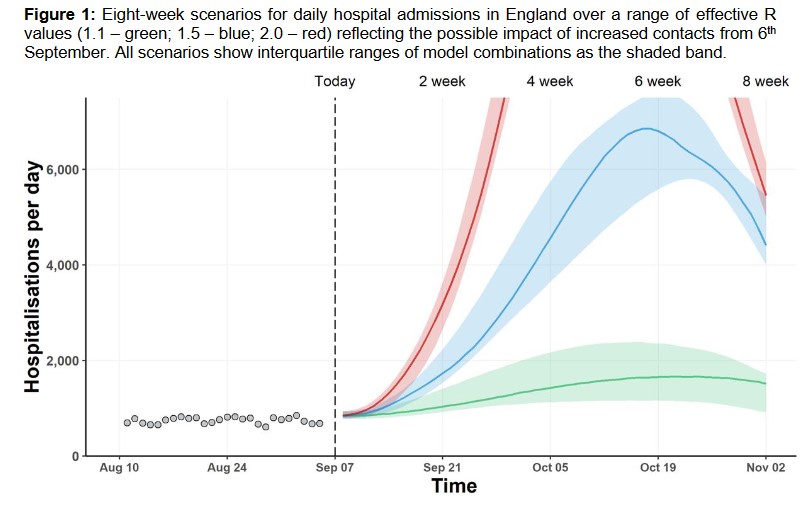
Chính phủ Anh có dự báo hàng tuần về số tử vong, số nhập viện. Họ có cả dự báo ngữ cảnh cho thời gian dài.
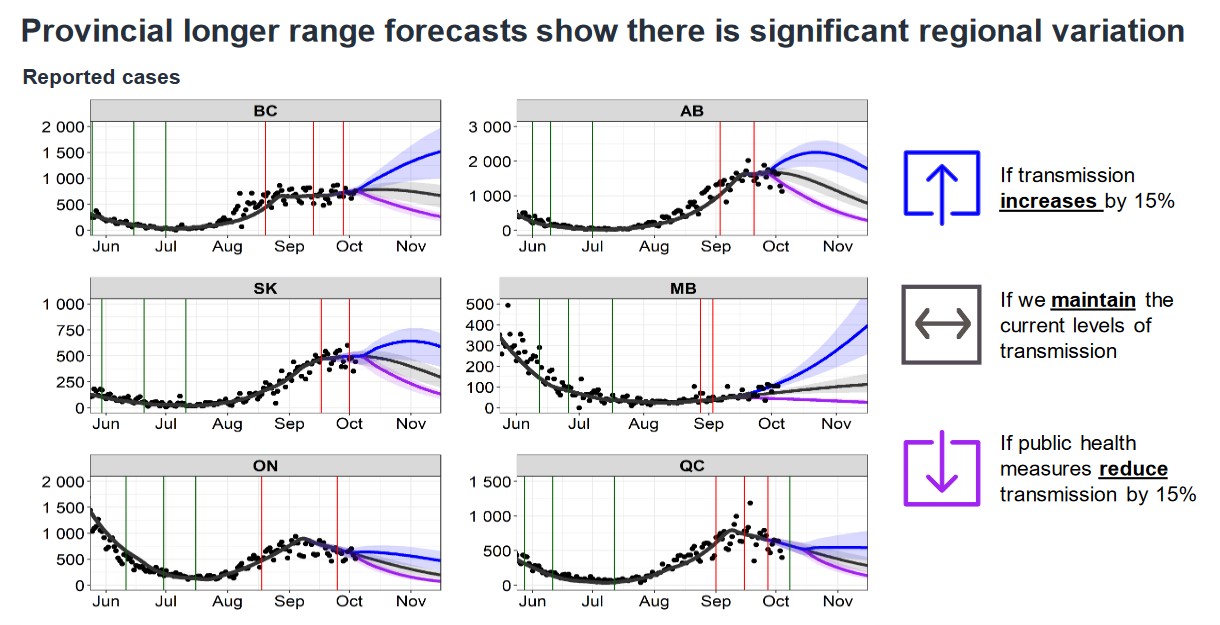
Chính phủ Canada sử dụng nhiều mô hình dự báo cho các mục đích khác nhau. Mỗi tháng thường có ít nhất một báo cáo.
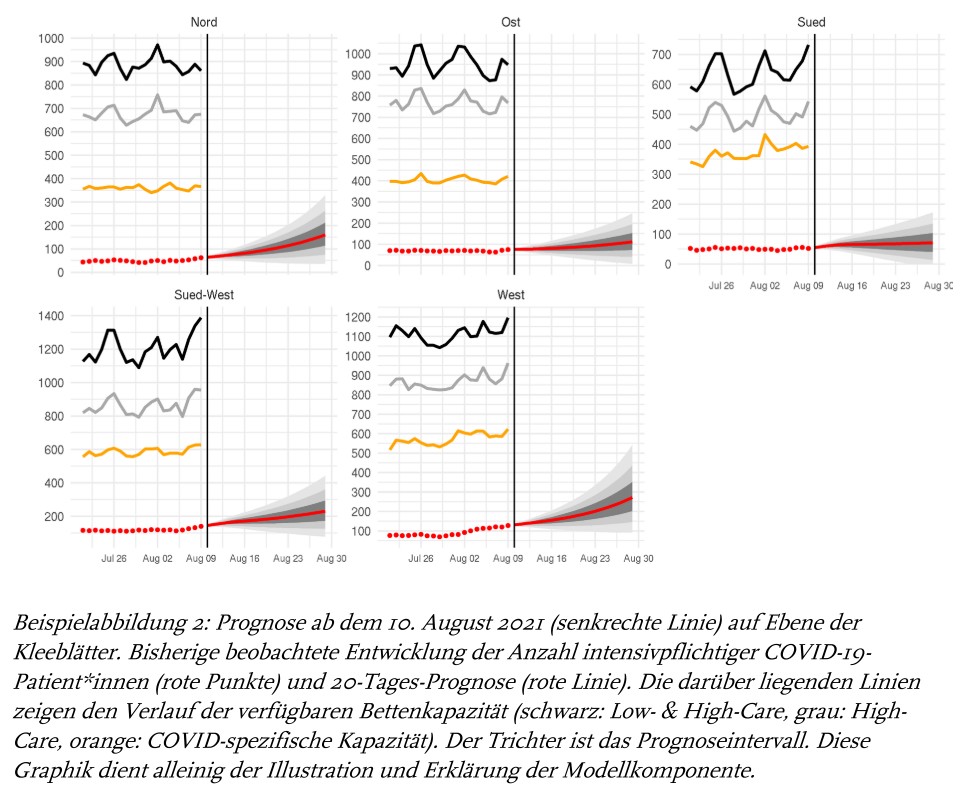
Chính phủ Đức có mô hình dự báo về số ca, số tử vong, số giường bệnh sẽ được sử dụng (4 loại giường bệnh theo các cấp độ khác nhau). Chỉ các nhân viên trong chính quyền mới được truy cập vào xem các dự báo. Ngoài ra Đức có một dashboard cho phép mọi người dân truy cập.
Chính phủ Mỹ sử dụng mô hình của hàng chục nhóm làm mô hình để xây dựng các mô hình dự báo cho số ca được báo cáo, số tử vong, số ca nhập viện.
4. Phụ lục
|
STT |
Ngày (2021) - Tài liệu |
|
1 |
27/05, Public Health England 2021 1 Dữ liệu: NHS Test and Trace data in UK. Distribution of time in days from contact exposure to secondary case onset of symptoms. Periods restricted to between 2 to 14 days. Household exposure dates are taken as date of onset or test in primary case. 618 household contact. 160 non-household contact. Phương pháp: Non-parametric Ước lượng T
Tác giả bình luận: không Nhận xét: Báo cáo 2 tuần sau Technical briefing 15 (11/06) với dữ liệu lớn hơn cho ước lượng median là 4 cho cả household và non-household. |
|
2 |
04/06, Pung et al. 2021 2 Dữ liệu: All house- hold transmission pairs involving individuals infected with the B.1.617.2 variant and notified between April 27 and May 22, 2021 in Singapore. 32 B.1.617.2 variant household transmission pairs. Phương pháp: Non-parametric Ước lượng T Median = 3 days Tác giả bình luận: This early investigation of recent B.1.617.2 variant cases offers no evidence to support a large difference (ie, >1 day) in serial intervals among the samples studied. Nhận xét: So sánh với chủng cũ (trước 07/04/2021) và ra cùng median, chỉ có mode là khác (2.7 so với 2 ngày). Ước lượng median cho T của chủng Delta nhỏ hơn 4, nhưng ước lượng đó của chủng trước cũng nhỏ hơn 4. Ước lượng ra 3 có thể do phương pháp không phù hợp. |
|
3 |
24/06, Zhang et al. 2021 3 Dữ liệu: 167 locally transmitted cases in Guangdong from May 21 to June 23. Used the initial 68 infections belonging to 24 clusters that had a clear chain of transmission. 21.6% (11/51) of serial intervals were negative. Phương pháp: Used gamma distributions and 51 transmission pairs. Ước lượng T Mean = 2.3 days (95% CI: 1.4–3.3) Tác giả bình luận: The estimated R0 (maximum likelihood method) was 3.2 (95% CI: 2.0–4.8). Rt increased from 3.0 to 3.5 from May 27 to May 29, then decreased after May 30, reached a value of 1 on June 6 Nhận xét: Ước lượng trung bình của T là 2,3 ngày. Có 1 số điểm cần xem xét. Một là dữ liệu nhỏ. Hai là nhiều KTGNT âm (21,6%) dẫn đến ước lượng của T nhỏ. Ba là có thể chưa điều chỉnh cho biến khác như tuổi (ví dụ người trẻ tuổi lây cho người cao tuổi và người cao tuổi nhanh đổ bệnh sẽ khiến KTGNT âm). Bốn là các ước lượng của R0 và các giá trị ban đầu của Rt nhỏ (ước lượng ra T càng nhỏ thì ước lượng cho R0 càng nhỏ). Năm là first author và nhiều đồng tác giả viết một bài khác với kết quả khác (First author trong bài mới này cũng là tác giả trong bài này). |
|
4 |
13/08, Kang et al. 2021 4 Dữ liệu: 167 patients infected with the Delta variant in the Guangdong outbreak in May-June 2021. Phương pháp: Gamma distribution. Time-varying forward serial intervals 5,6. Ước lượng T Giảm dần từ 5.8 ngày. Sau khoảng 10 ngày thì hầu như bằng 4 ngày. Tác giả bình luận: không Nhận xét: Như vậy báo cáo ngày 24/06 của Zhang et al. 2021 3 đã coi như bị hủy bỏ. |
|
5 |
06/10, Ryu et al. 2021 7 Dữ liệu: 82,671 local cases from 11 Jul through 1 Sep, when the Delta variant accounted for more than 40%. Because the Delta variant accounted for more than 50% after 25 Jul, divided the study period into two periods (Period 1: 11-24 Jul and Period 2: 25 Jul-15 Aug). Used 3728 transmission pairs (out of a total 5063 pairs) having the date of symptom onset for both infector and infectee (1,344 pairs in Period-1 and 2,384 pairs in Period-2). Phương pháp: Normal distribution. Ước lượng T Period 1: Mean = 3.7 days (95% CrI: 3.5, 3.8). Period 2: Mean = 3.5 days (95% CrI: 3.4, 3.6). Tác giả bình luận: không Nhận xét: Đây là phiên bản 2. Phiên bản 1 vào ngày 20/8 ước lượng T giai đoạn 2 chỉ 2.46. Dựa vào số cặp truyền bệnh được đề cập, có thể tác giả nhầm lẫn dữ liệu giữa các giai đoạn 1 và 2 nên dẫn tới sai sót. Trong phiên bản cũ, có 53896 ca từ 11/7 đến 14/8. Giai đoạn 2 từ 25/7-15/8. Có 3271 cặp truyền bệnh, trong đó 1672 và 1599 cặp tương ứng cho giai đoạn 1 và 2. Ước lượng của T cho giai đoạn 1 và 2 tương ứng là 3,95 và 2,46 ngày. Trong phiên bản mới, 1344 và 2384 cặp tương ứng cho giai đoạn 1 và 2. Số cặp cho giai đoạn 2 trong bản mới khác hẳn bản cũ. |
Tài liệu tham khảo
1. Public Health England. SARS-CoV-2 variants of concern and variants under investigation in England - Technical briefing 13 (27 May 2021). (2021).
2. Pung, R., Mak, T. M., CMMID COVID-19 working group, Kucharski, A. J. & Lee, V. J. Serial intervals in SARS-CoV-2 B.1.617.2 variant cases. Lancet (London, England) 398, 837–838 (2021).
3. Zhang, M. et al. Transmission Dynamics of an Outbreak of the COVID-19 Delta Variant B.1.617.2 — Guangdong Province, China, May–June 2021. China CDC Wkly. 3, 584–586 (2021).
4. Kang, M. et al. Transmission dynamics and epidemiological characteristics of Delta variant infections in China. medRxiv 2021.08.12.21261991 (2021). doi:10.1101/2021.08.12.21261991
5. Ali, S. T. et al. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science (80-. ). 369, 1106–1109 (2020).
6. Park, S. W. et al. Forward-looking serial intervals correctly link epidemic growth to reproduction numbers. Proc. Natl. Acad. Sci. U. S. A. 118, (2021).
7. Ryu, S., Kim, D., Lim, J.-S., Ali, S. T. & Cowling, B. J. Serial interval and transmission dynamics during the SARS-CoV-2 Delta variant predominance in South Korea. medRxiv 2021.08.18.21262166 (2021). doi:10.1101/2021.08.18.21262166
Bình luận:
Chưa có bình luận nào.